Additionneur non-inverseur (extensible à n entrées)

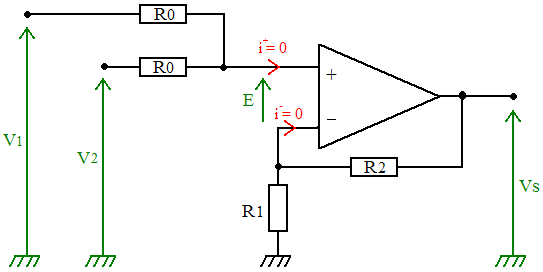
a) schéma

b) formule

OU

c) Remarques

A partir de ce schéma on peut rajoutez autant de tension d'entrées que nécessaire (à condition de rajoutez autant de résistance R₀).
La résistance de chaque entrée vaut au moins R₁.

Comment calculer Vs en fonction de Ve

Pour ce calcul, on va considérer un montage additionneur non-inverseur avec 2 entrées (V1 et V2)

Comme pour d'autres montages de l'AOP, nous pouvons dire qu'avec cet additionneur non-inverseur on a:

• Un fonctionnement linéaire
• Un AOP supposé parfait, donc E=0V, ainsi V+=V-

Alors, pour déterminer Vs de l'additinneur non-inverseur il faut déterminer V+ et V- de l'équation V+=V-:

• Calcul de V+: A l'aide du théorème de Millman on peut en déduire cette formule:
  => =>
• Calcul de V-: A l'aide du diviseur de tension on peut déduire cette formule:
  

Sachant que V+=V-, on a:

Il est judicieux maintenant d'isoler Vs de l'additionneur non-inverseur:

=>

Nous avons ainsi déterminer la formule de l'additionneur non-inverseur à 2 entrées. Pour n entrées nous aurions eu cette formule:

Le montage porte le nom d'additionneur non-inverseur car il additionne les tensions d'entrées sans les inverser